Volume Formulas: A Complete Guide

Introduction

Understanding volume formulas is essential for solving mathematical problems in geometry, physics, and real-world applications. Volume measures the space occupied by a 3D object. In this guide, we will cover the most important volume formulas with examples to help you master the concept.

Basic Volume Formulas

Below are the volume formulas for commonly used 3D shapes:

1. Cube

A cube has six equal square faces. The formula for its volume is:\(𝑉=𝑎^3\) where

$a$

is the length of a side.

 2. Rectangular Prism (Cuboid)

A cuboid has different length, width, and height. The volume formula is: \(V=l\times w\times h\) where \(l\) is length, $w$ is width, and $h$ is height.

3. Cylinder

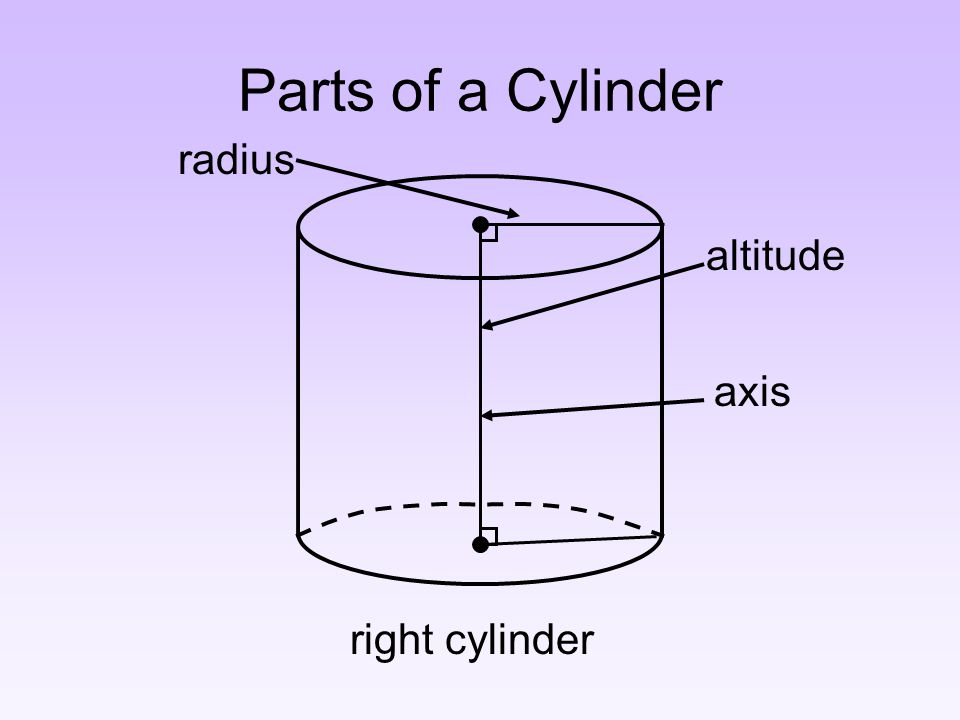
A cylinder has two circular bases and a curved surface. The volume formula is: \(V=𝜋𝑟^2 h\) where

$r$ is the radius of the base and $h$ is the height.

4. Sphere

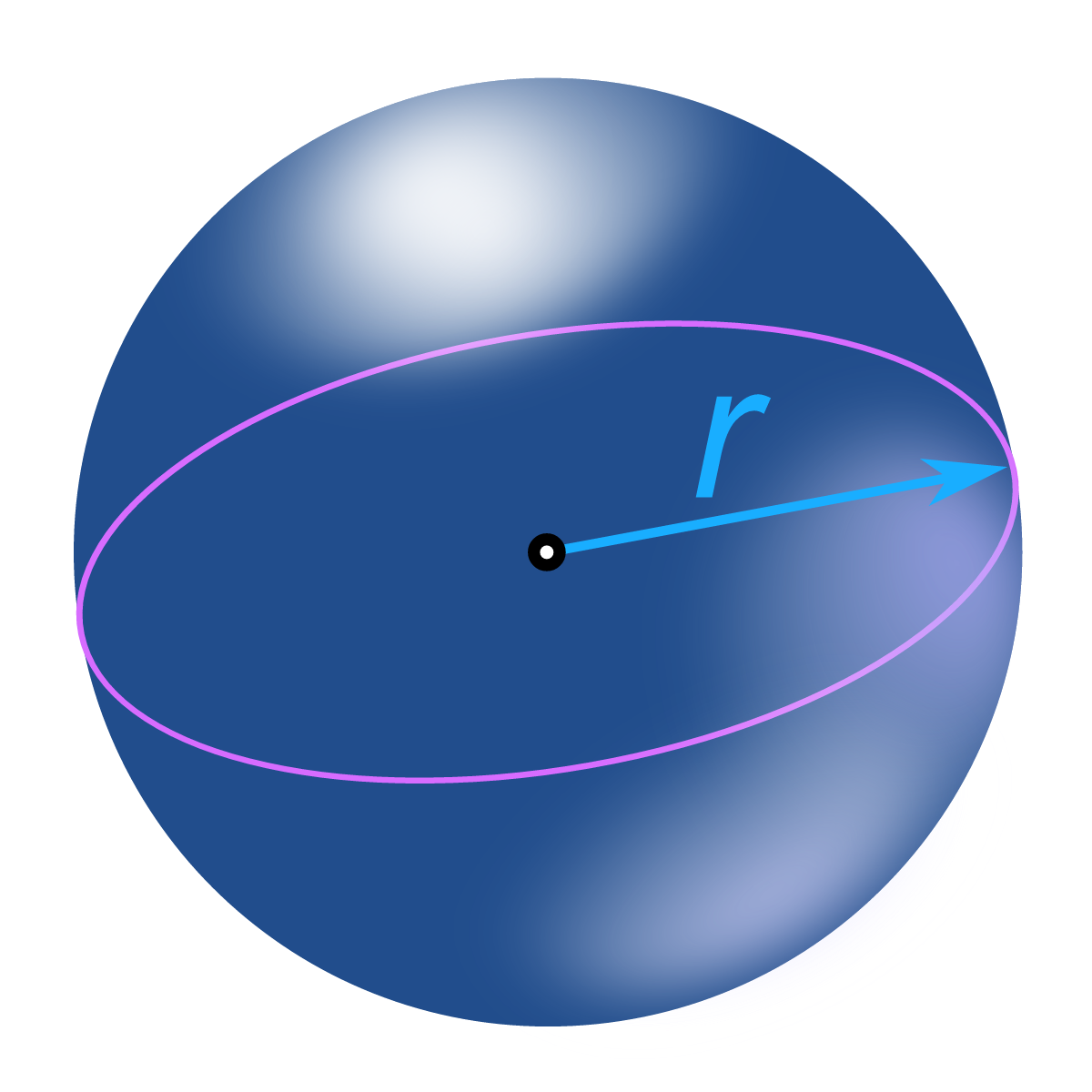
A sphere is a perfectly round 3D object. Its volume formula is: \(V=\frac{4}{3}𝜋𝑟^3\) where $r$

is the radius.

5. Cone

A cone has a circular base and tapers to a point. The volume formula is: $V = \frac{1}{3} \pi r^2 h$ where $r$ is the base radius and $h$ is the height.

6. Pyramid

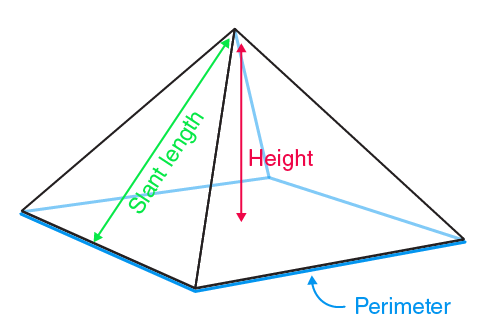
A pyramid has a polygonal base and triangular faces that meet at a single point. The formula for its volume is:

$V = \frac{1}{3} B h$ where $B$ is the area of the base and $h$ is the height.

Advanced Volume Formulas

7. Hemisphere

A hemisphere is half of a sphere. Its volume formula is: \(V=\frac{2}{3}𝜋r^3\) where $r$ is the radius.

8. Ellipsoid

An ellipsoid is an elongated sphere. The formula for its volume is: \(V=\frac{4}{3}𝜋𝑎𝑏𝑐\) where$\mathrm{\backslash (a\backslash ), <span\; style="font-family:\; Georgia,\; \text{'}Times\; New\; Roman\text{'},\; \text{'}Bitstream\; Charter\text{'},\; Times,\; serif;">\; </span>}$ $b$,  and $c$ are the semi-axes.

Real-Life Applications of Volume Formulas

1. Construction: Architects and engineers use volume formulas to calculate material requirements.
2. Storage and Packaging: Companies determine the space needed for products.
3. Water Tanks: Volume calculations help estimate water capacity.
4. Medical Industry: Used in drug formulation and medical imaging.

Conclusion

Knowing volume formulas is crucial for solving practical and theoretical problems. Whether you are a student or a professional, mastering these formulas will help you in various fields. These formulas are also foundational for advanced academic exams like JEE (Joint Entrance Examination) and NEET (National Eligibility cum Entrance Test), where geometry and 3D calculations are essential parts of the syllabus. A solid understanding of volume formulas is crucial for excelling in these exams and beyond, especially for future careers in engineering, medicine, architecture, and physics. Keep practicing with different examples to strengthen your understanding and improve your problem-solving skills!